A couple of months ago I was on a flight and had a thought: How far is the horizon at this very moment?
I got my notebook and pen out and tried to solve this using only the knowledge I had, since there was no internet anyway. Of course, many assumptions were made as were convenient for the calculation.
I planned on checking my answer once I landed. If you want to attempt it, stop reading here and come back later when you have a solution. Unfortunately for me, I made a little error subtracting between two big numbers and got a completely wrong answer.
Assumptions
I assumed the following
- Perfect visibility, no degradation due to atmosphere
- Earth is a perfect sphere with a radius of 6400km
- Aeroplane flying at an altitude of 10km
Solution
Thanks to the assumptions, the problem reduces to primary school geometry problem and is trivial to solve once visualized clearly on a piece of paper.
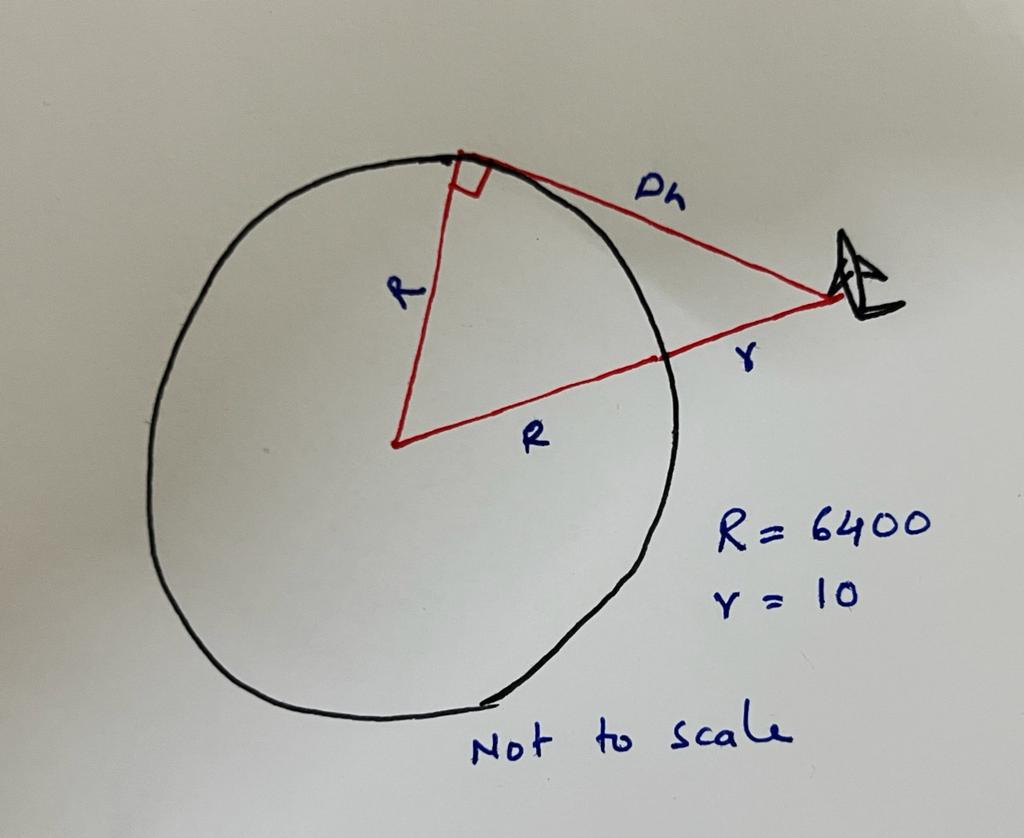
Using Pythagoras Theorem we know how to calculate the third side of a right angled triangle give the first two. We also know that a tangent to a circle (the line of sight from an aeroplane) meets the circle in a way that it is perpendicular to the radius drawn from the point of contact.
Combining the two pieces of knowledge, the problem can be trivially arranged as follows
(R + r)² = R² + Dh²
Where
- R is the radius of the earth (in Kilometers)
- r is the distance of the aeroplane from the surface of the earth (in Kilometers)
- Dh is the distance to the horizon
Rearranging, we get
Dh² = (R + r)² – R²
Expanding the (a + b)² equation
Dh² = R² + 2Rr + r² – R²
Dh² = 2Rr + r²
Taking square root on both sides
Dh = √(2Rr + r²)
Substituting the values
Dh = √(2*6400*10 + 10²)
Dh = √(128000 + 100)
Dh = √(128100)
Dh = 357.9
Distance to horizon is about 358 kilometers when the aeroplane is at an altitude of 10 kilometers. Now looking at the map while sitting in a flying aeroplane is a lot more insightful as I can guess which cities I’m looking at outside the window.
That’s it for this little post. Thank you for reading!